[LG]《Learning on the Manifold: Unlocking Standard Diffusion Transformers with Representation Encoders》A Kumar, V M. Patel [Johns Hopkins University] (2026)
这篇关于扩散模型(Diffusion Models)底层逻辑的深度研究,挑战了当前大模型开发中“暴力出奇迹”的固有认知。
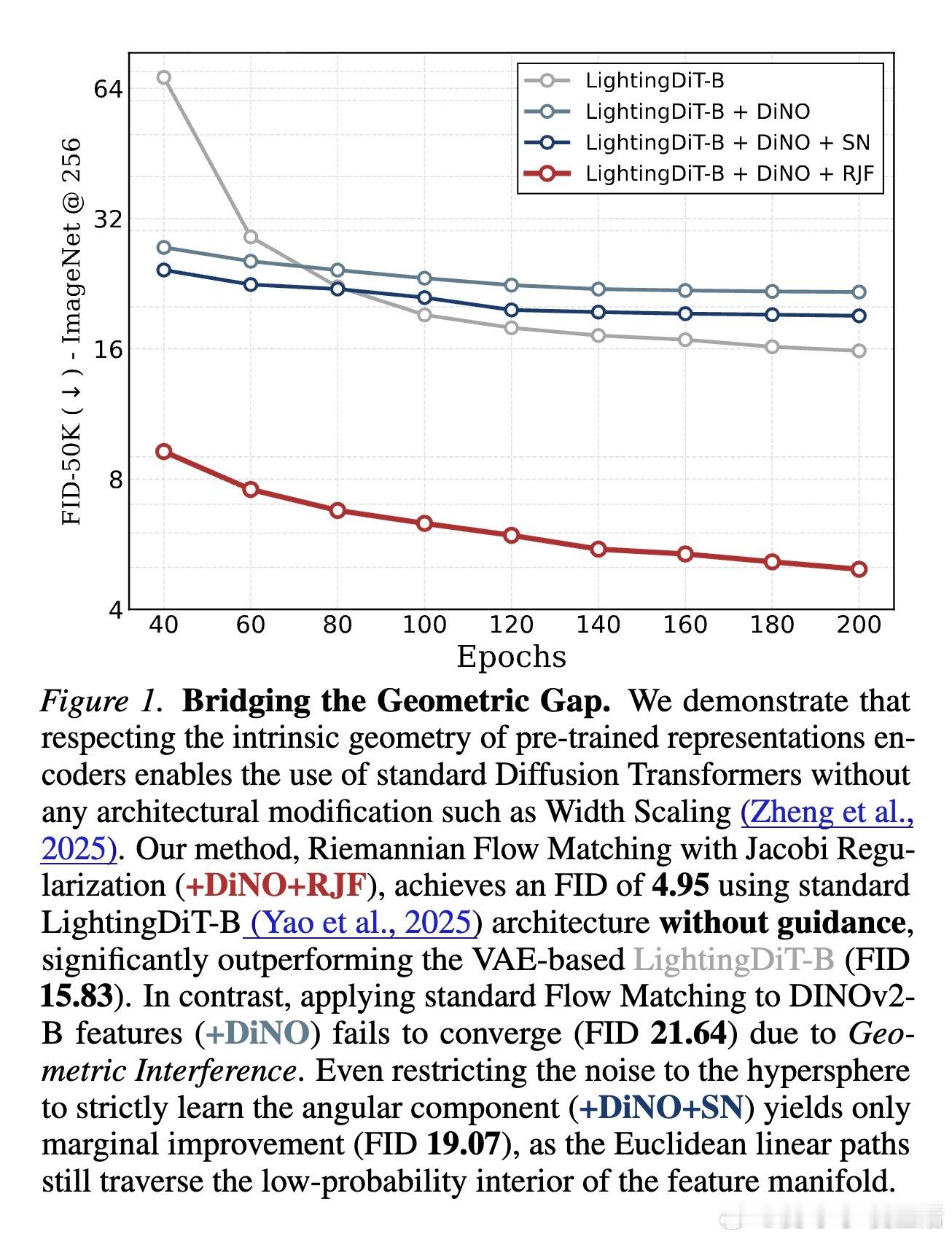
生成模型的范式正在发生演变:从像素空间转向潜在空间,再到直接在DINOv2或SigLIP等预训练特征上进行生成。然而,研究者们发现一个诡异的现象:标准的扩散transformer(DiT)在这些高维语义特征上极难收敛。此前的观点认为这是“容量瓶颈”,主张通过增加模型宽度来硬扛。但最新研究指出:这并非模型不够大,而是我们走错了路。
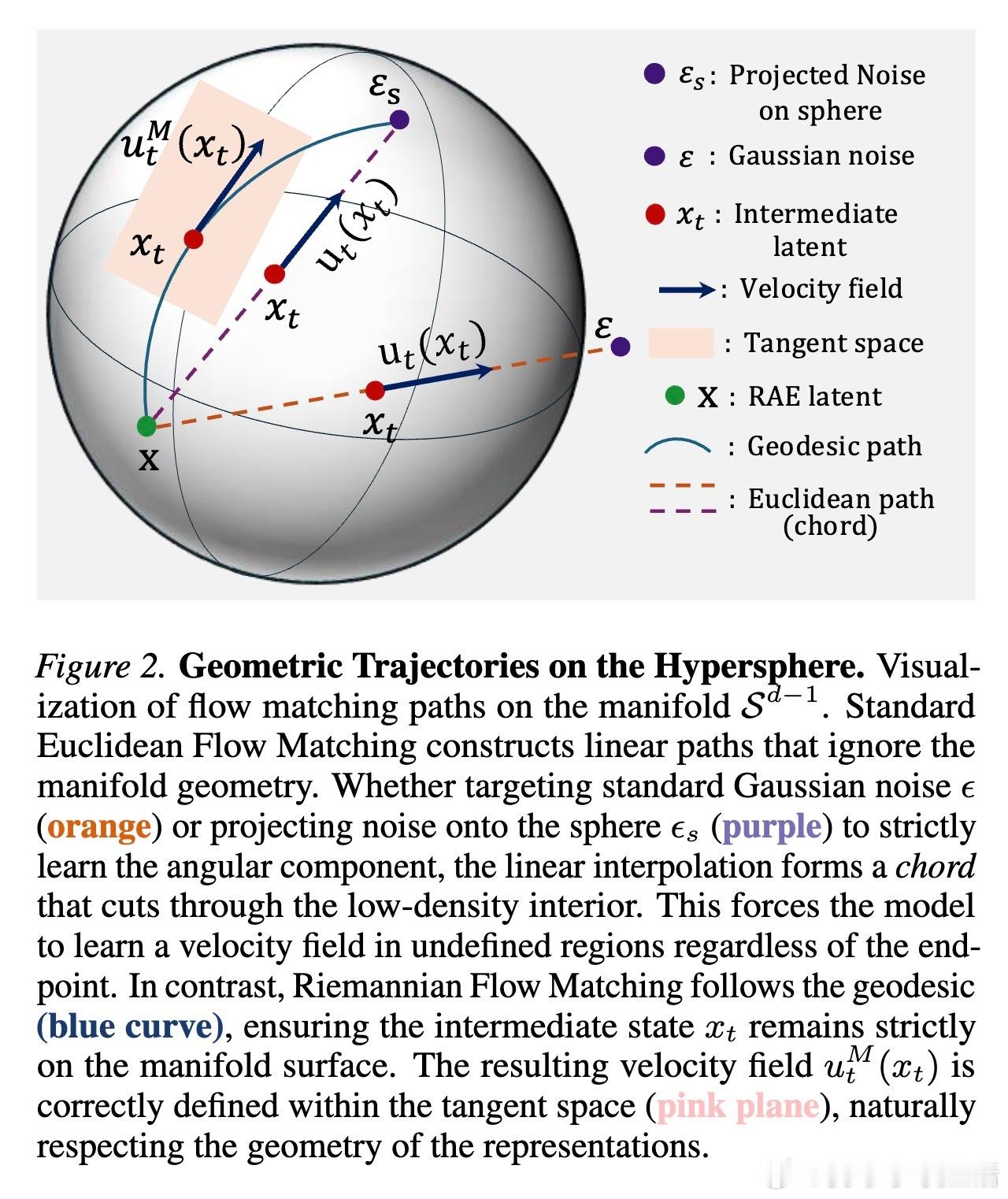
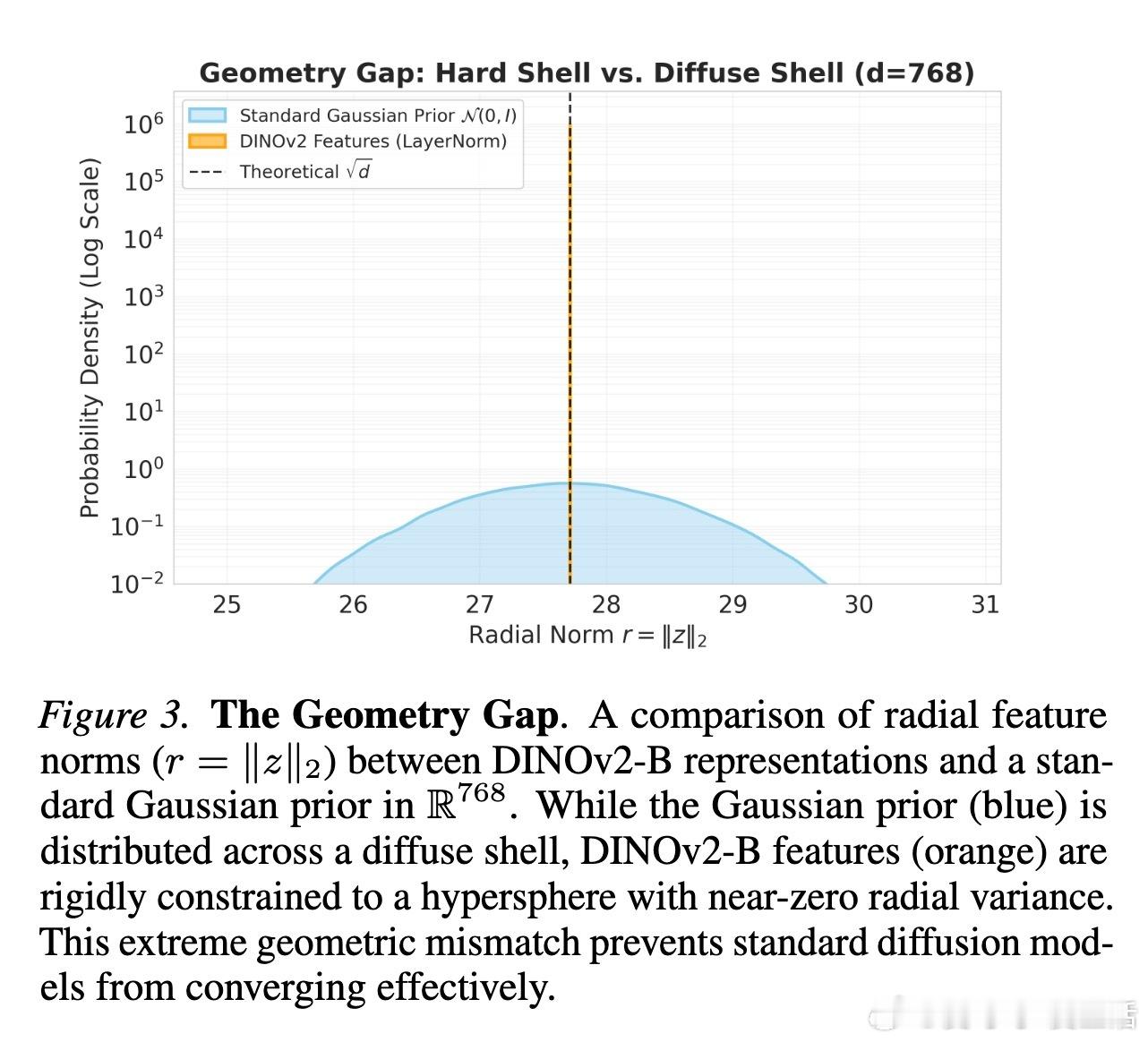
问题的核心在于几何干涉。研究发现,DINOv2等编码器的特征并非散落在平坦的欧几里得空间,而是严格分布在一个超球面上。标准的流匹配算法(Flow Matching)假设路径是两点间的直线,这在球面上就像是一根穿透球体的“弦”。这条路径被迫经过特征分布极稀疏、甚至未定义的球体内部真空区。模型在这些“无主之地”苦苦寻找梯度,最终导致训练崩溃。
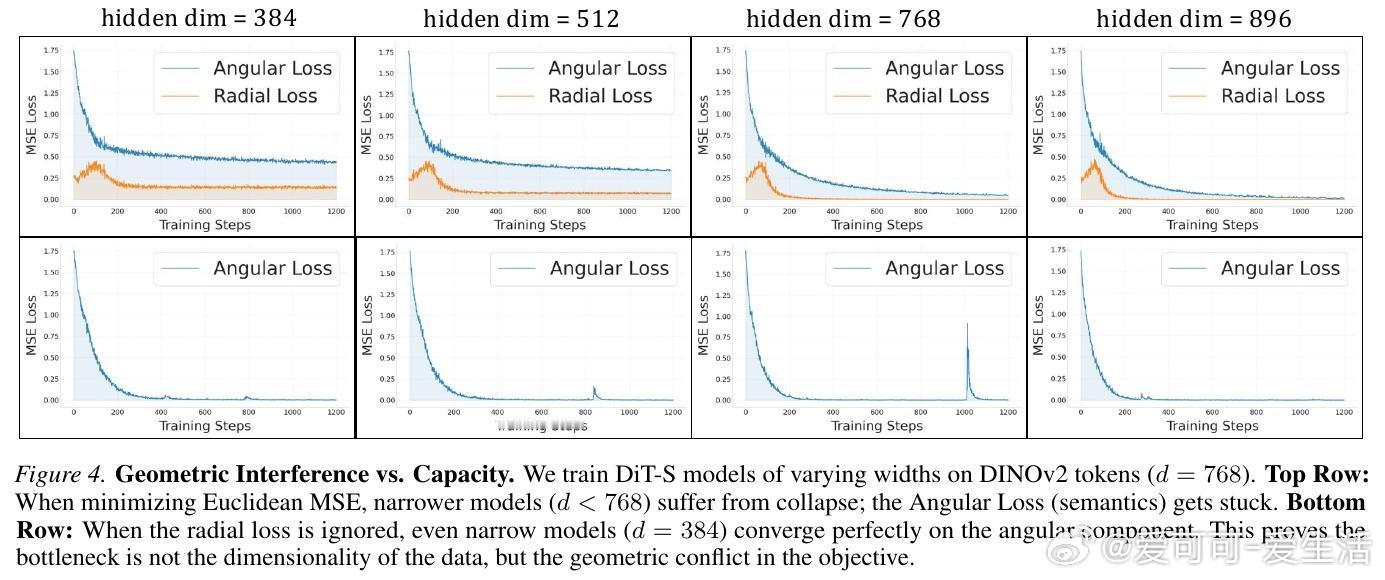
为了验证这一猜想,作者做了一个极具启发性的实验:他们将损失函数分解为径向(长度)和角向(方向)。结果显示,即使是参数量极小的模型,只要不强迫它去学习那个违背几何规律的径向分量,它就能瞬间学会复杂的语义。这意味着,所谓的“宽度缩放”其实是在浪费算力,让模型去强行记忆那些本不该存在的无效路径。
针对这一几何鸿沟,论文提出了RJF(黎曼流匹配与雅可比正则化)框架。首先,用球面线性插值(SLERP)取代直线插值,确保生成路径始终贴合在流形表面滑动。其次,引入雅可比正则化来修正曲率引起的误差传播。这就像是把在荒野中横冲直撞的越野车,引导到了顺滑的环形高速公路上。
这种对几何结构的尊重带来了效率的飞跃。仅有1.31亿参数的标准DiT-B模型,在不改变架构的情况下成功收敛,FID达到3.37,而此前的方法在同等规模下几乎无法工作。在更大规模的DiT-XL上,RJF仅用80个epoch就超越了其他训练更久、甚至带有复杂对齐损失的SOTA模型。
这带给我们一个深刻的思考:在追求Scaling Laws的道路上,我们是否过度依赖了算力的堆砌,而忽视了数据本身的内在流形?生成模型的本质是寻找概率分布之间的最优路径。如果路径本身违背了空间的拓扑结构,再大的模型也只是在虚无中挣扎。
总结:算法的平庸往往需要通过参数的冗余来补偿。尊重数据的几何本能,比盲目扩张模型的边界更重要。生成不是在真空中造物,而是在流形的表面起舞。
论文链接:arxiv.org/abs/2602.10099