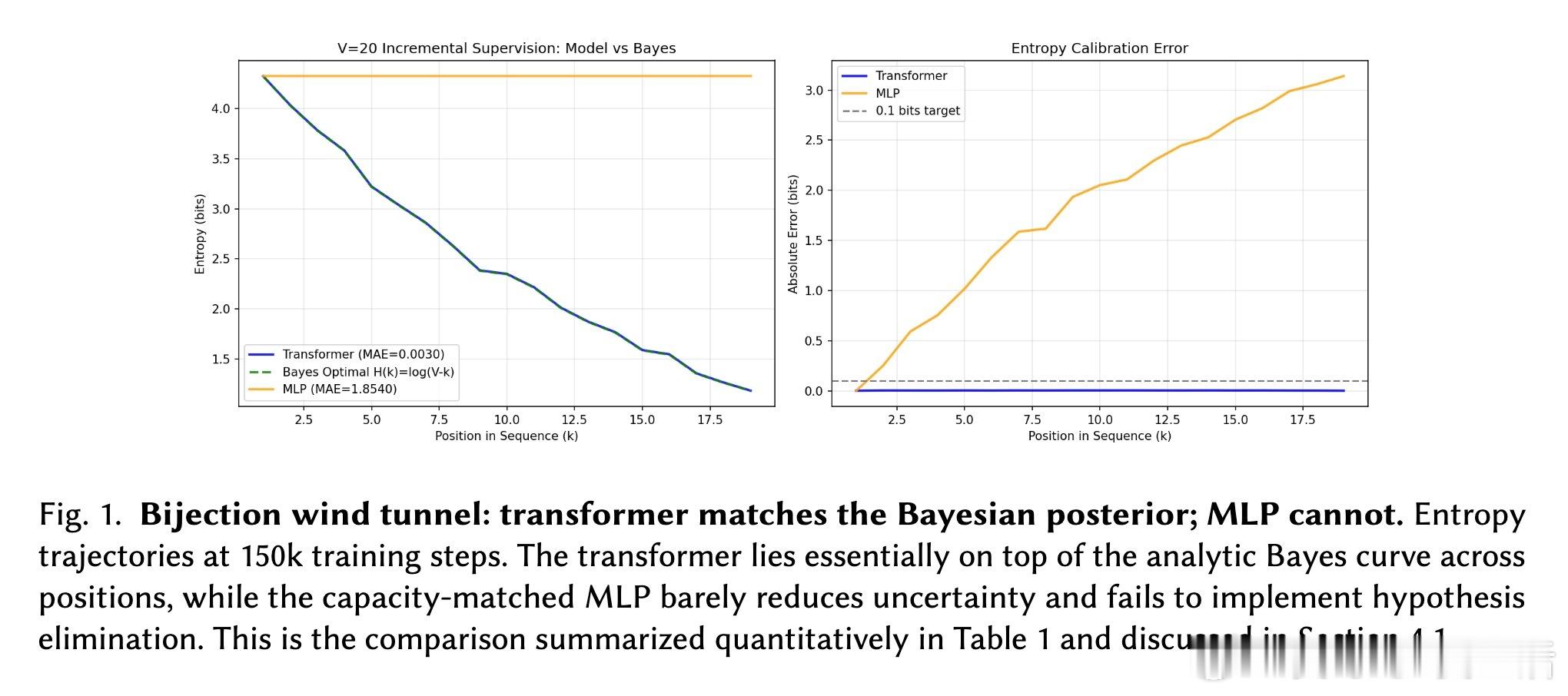
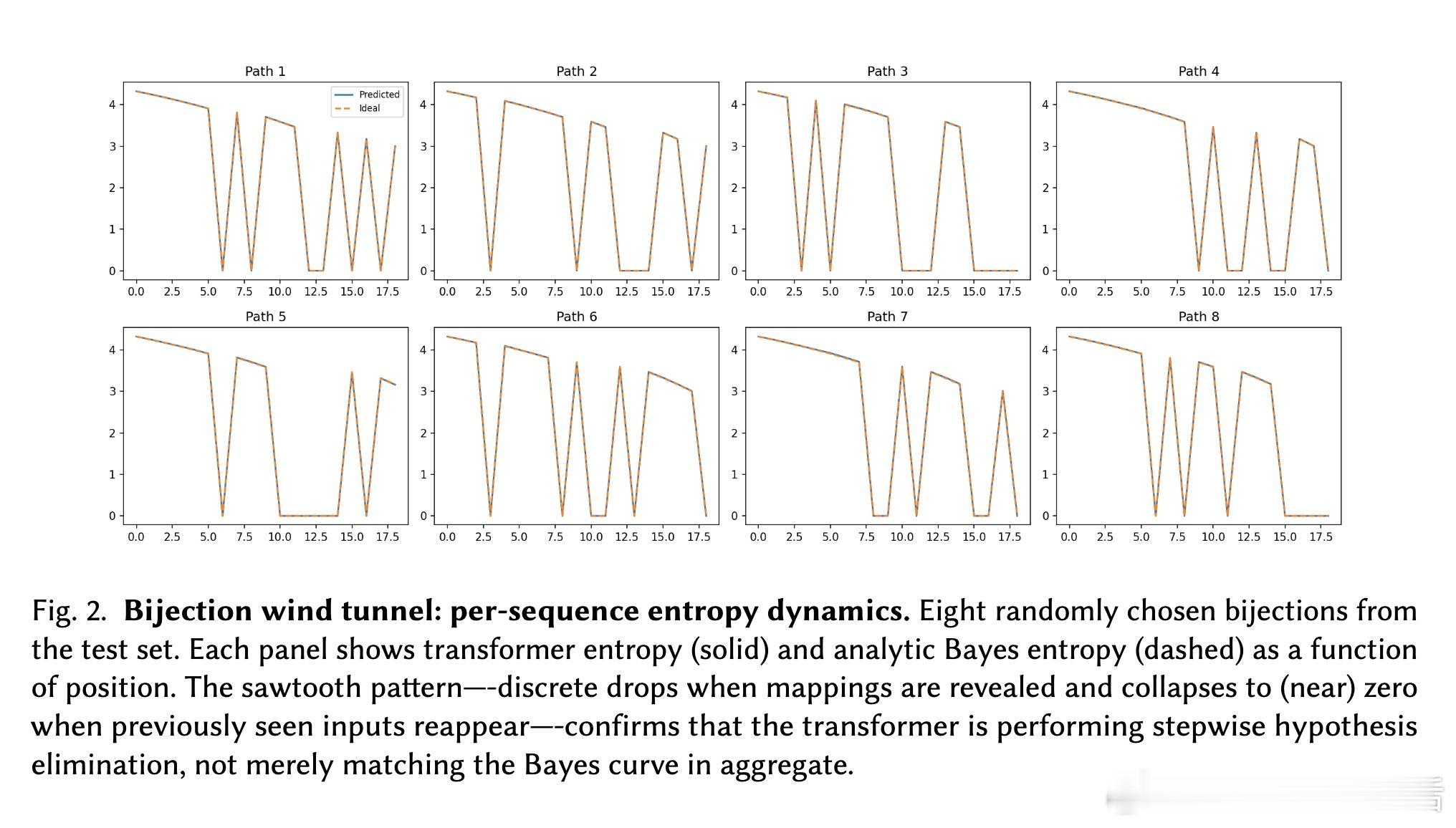
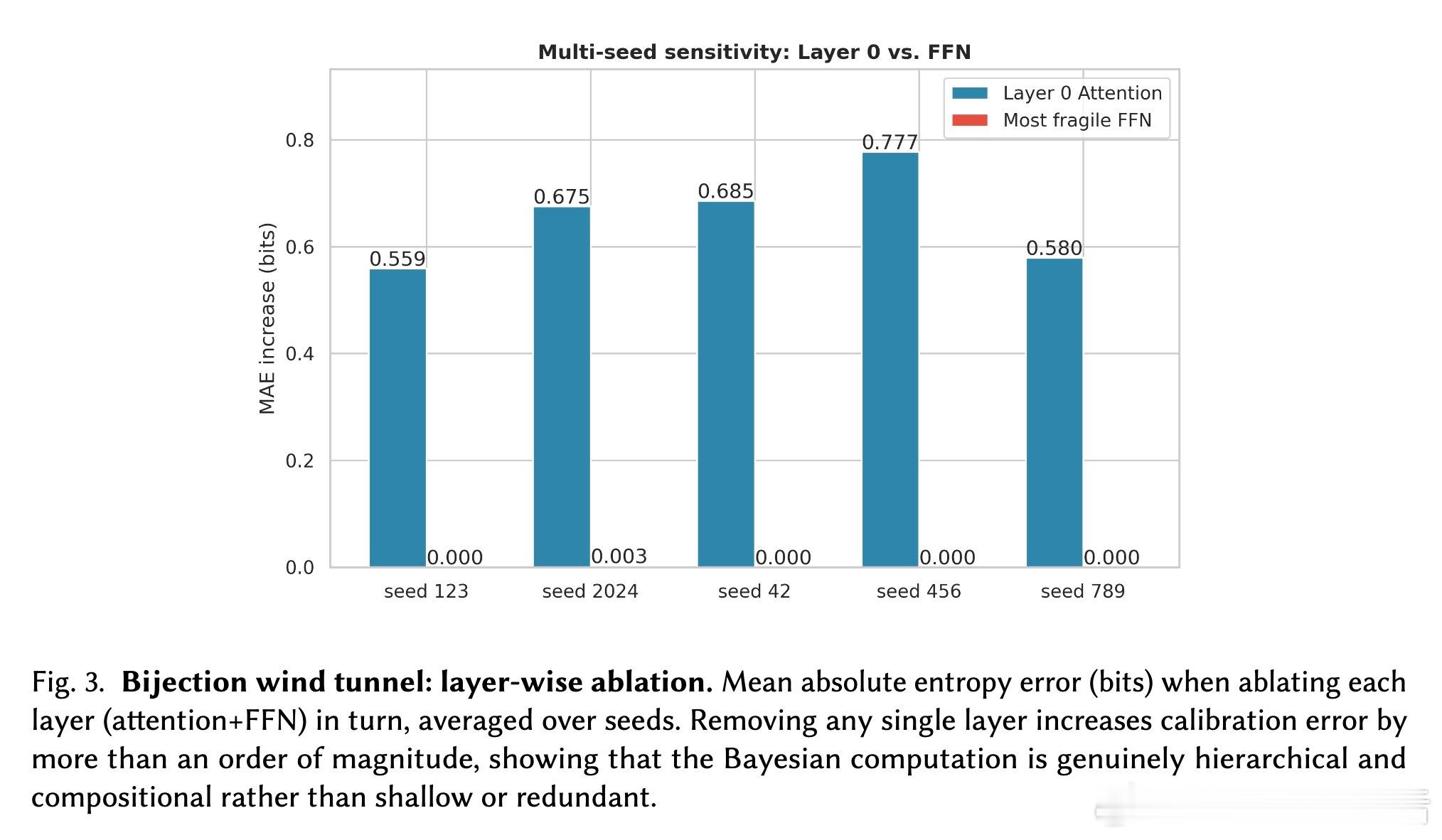
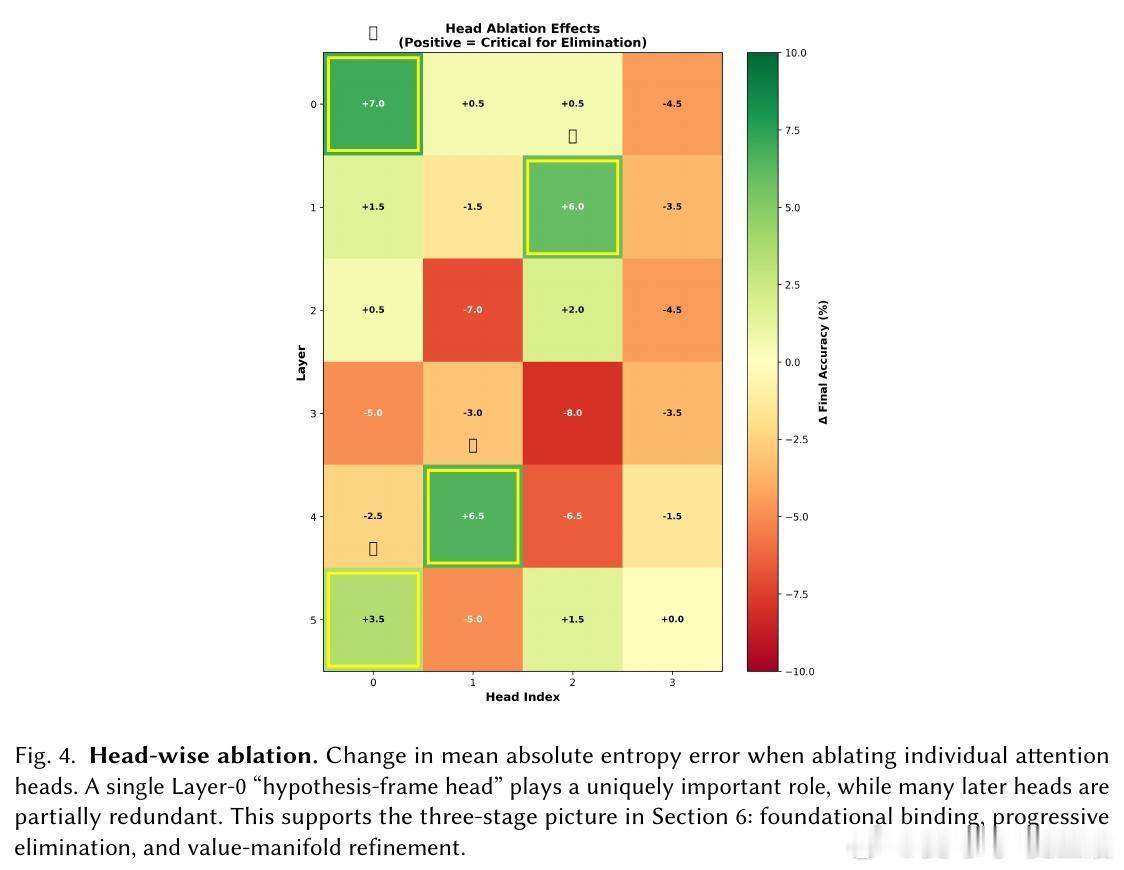
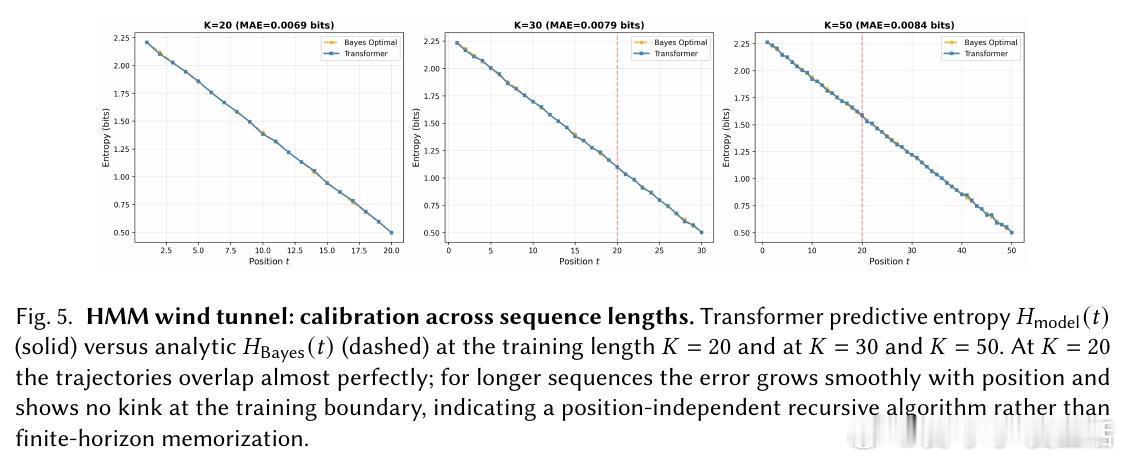
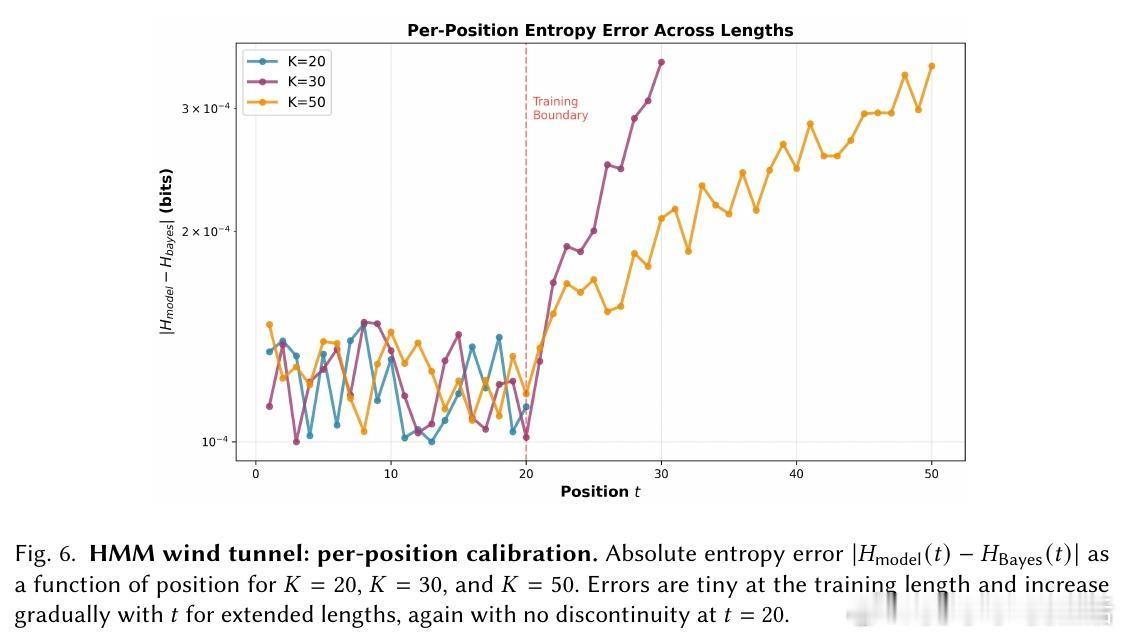
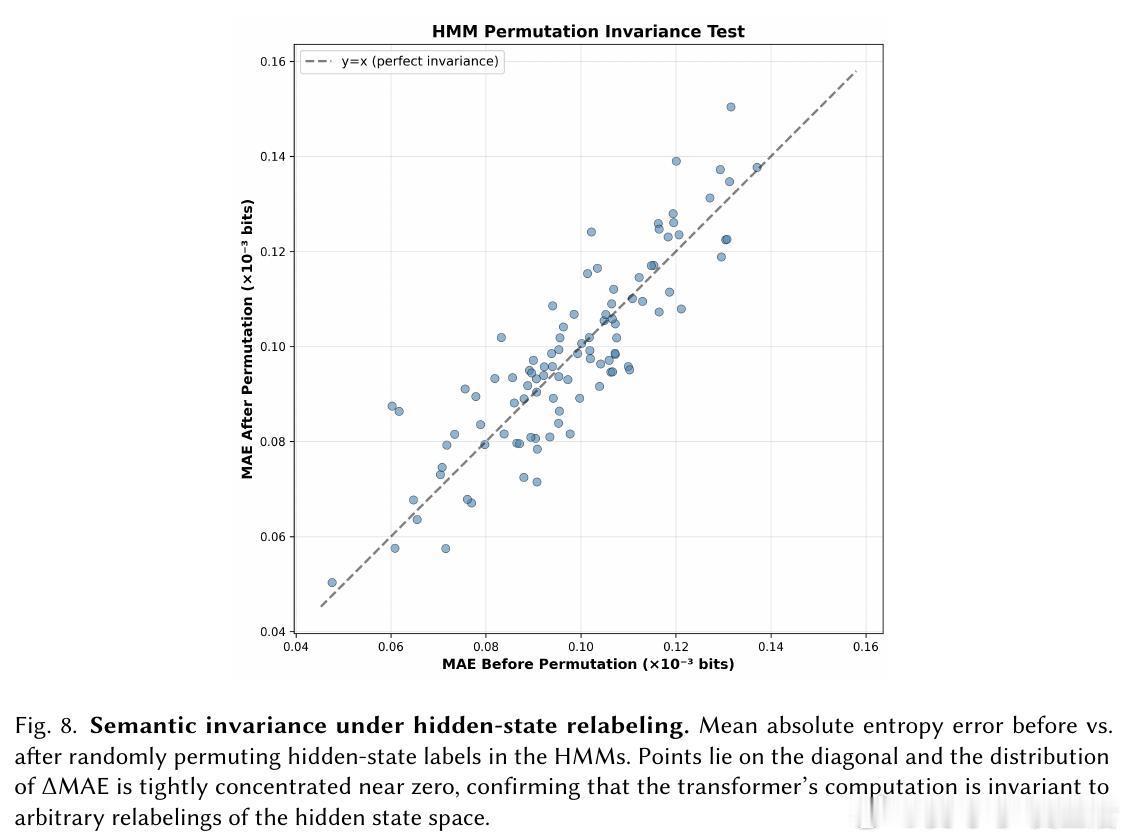
[LG]《The Bayesian Geometry of Transformer Attention》N Aggarwal, S R. Dalal, V Misra [Dream Sports & Columbia University] (2025) Transformer究竟是在进行真正的贝叶斯推理,还是仅仅通过模式匹配在“演”一种逻辑?长期以来,由于自然语言缺乏解析后验概率,我们无法区分模型是在进行概率计算还是在依赖记忆。这篇来自哥伦比亚大学等机构的论文《The Bayesian Geometry of Transformer Attention》通过构建“贝叶斯风洞”,为我们揭开了Transformer内部几何设计的奥秘。什么是“贝叶斯风洞”?研究者设计了两个受控环境:双射学习和隐马尔可夫模型(HMM)状态跟踪。在这些环境中,真实的后验概率有精确的闭式解,且假设空间巨大,模型绝无可能通过记忆过关。这把一个模糊的定性问题转化为了定量测试:模型的预测熵是否在每一个位置都与解析后的贝叶斯熵吻合?实验结果令人震撼。仅有200万参数的小型Transformer在预测精度上达到了10^-3至10^-4比特的极高准确度,几乎与数值计算的误差相当。相比之下,参数量完全匹配的MLP在同样的任务中彻底溃败。这证明了Transformer的成功并非单纯来自规模,而是源于其独特的架构偏置。Transformer是如何在内部实现贝叶斯的?研究揭示了一个清晰的三阶段几何机制:第一阶段,基础绑定(Layer 0)。Layer 0的注意力机制通过正交的Key向量构建了一个“假设框架”。这相当于在残差流中建立了一套坐标系,为后续的推理提供了结构化的基质。第二阶段,序列消除(中间层)。随着深度增加,Query和Key的对齐变得越来越尖锐。这在几何上对应于贝叶斯更新中的“证据集成”:模型逐层剔除不符合观察结果的假设,将注意力集中在可行的子空间。第三阶段,精度精炼(顶层)。在路由结构稳定后,最后的层级在低维流形上展开,对后验概率进行微调。研究发现,价值空间(Value-space)会演化成一个由后验熵参数化的平滑流形。这里有一个深刻的洞察:框架与精度的解耦。在训练过程中,注意力模式(路由)会较早稳定下来,确定“信息去往何处”;而价值表征(精度)则会持续演化,直到能精确编码信念的细微差别。这种“先定框架,再磨精度”的动力学过程,解释了Transformer处理复杂推理时的稳健性。为什么MLP会失败?因为MLP缺乏内容寻址的路由能力和残差组合性。贝叶斯推理本质上是一个层次化的精炼过程,Transformer通过残差流承载信念状态,通过FFN执行数值更新,通过注意力进行内容寻址。这种几何设计与贝叶斯公式的结构达成了完美的同构。这项研究为我们理解大模型提供了一个“可验证的下限”。如果一个模型在闭式解明确的风洞中都无法实现贝叶斯,那么它在处理自然语言时的逻辑便不可信。Transformer的成功告诉我们,推理不仅仅是数据的堆砌,更是几何上的必然。论文链接:arxiv.org/abs/2512.22471