小学奥数：几何模型知识点全面汇总✅太全了

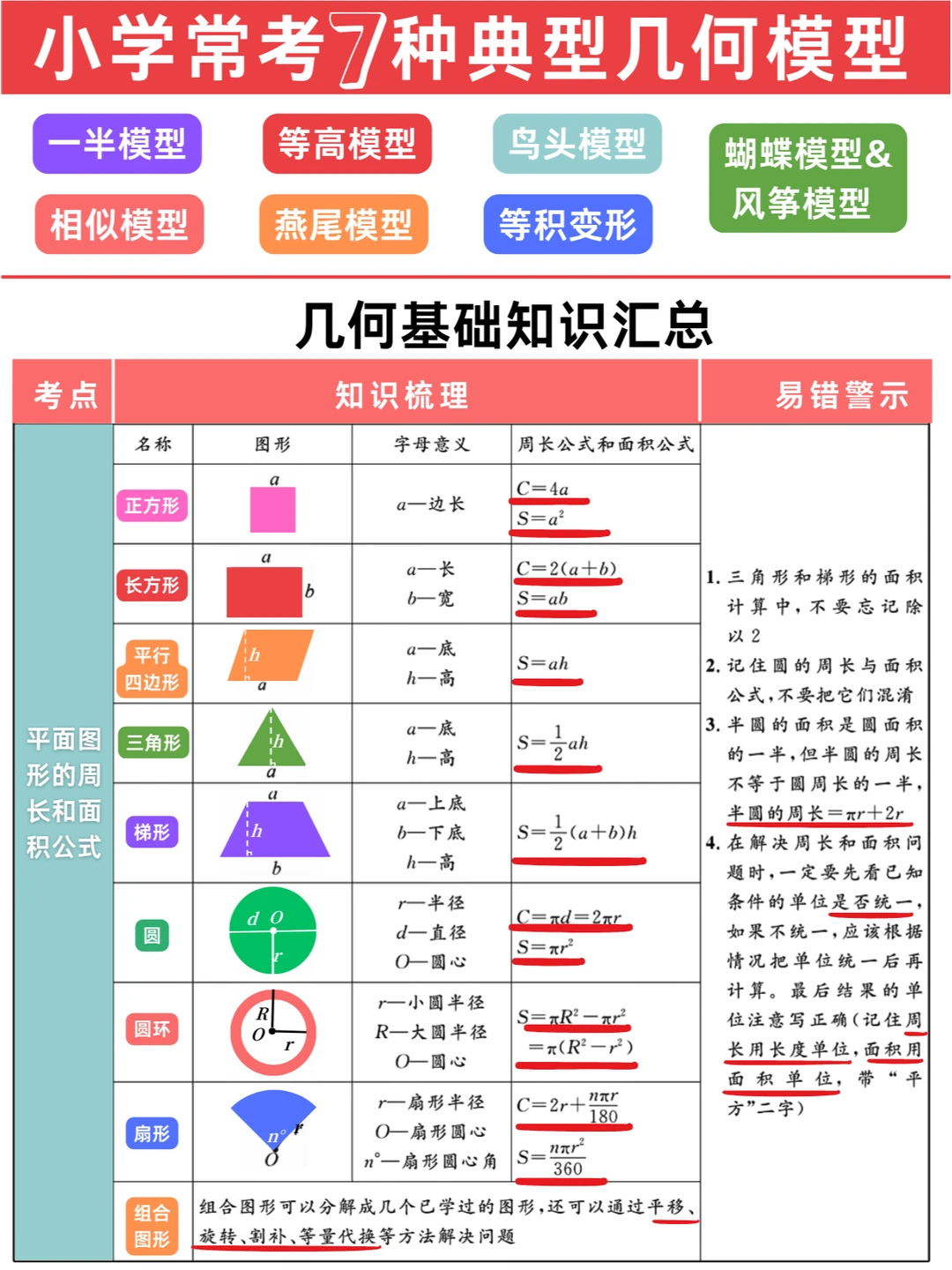
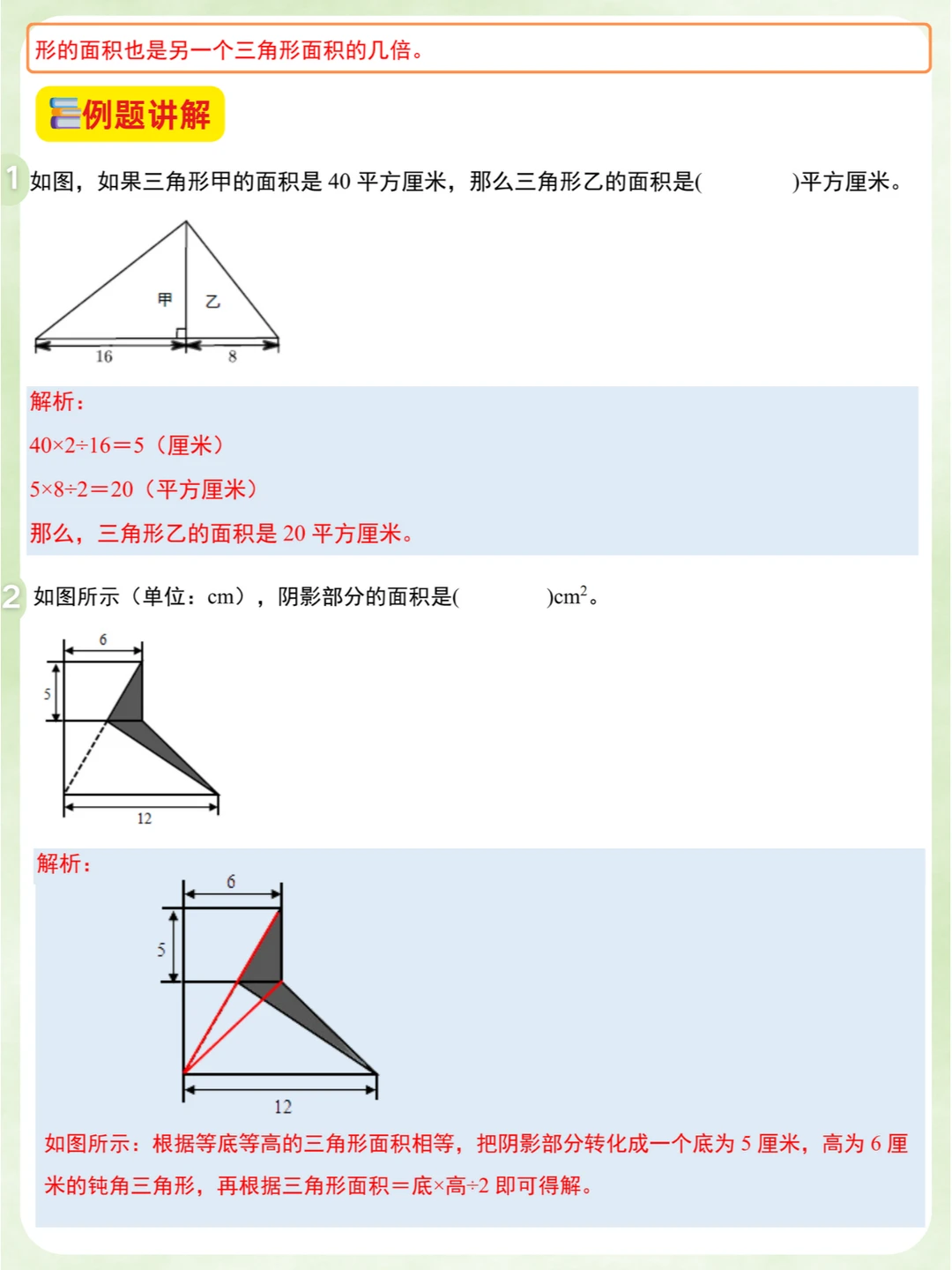
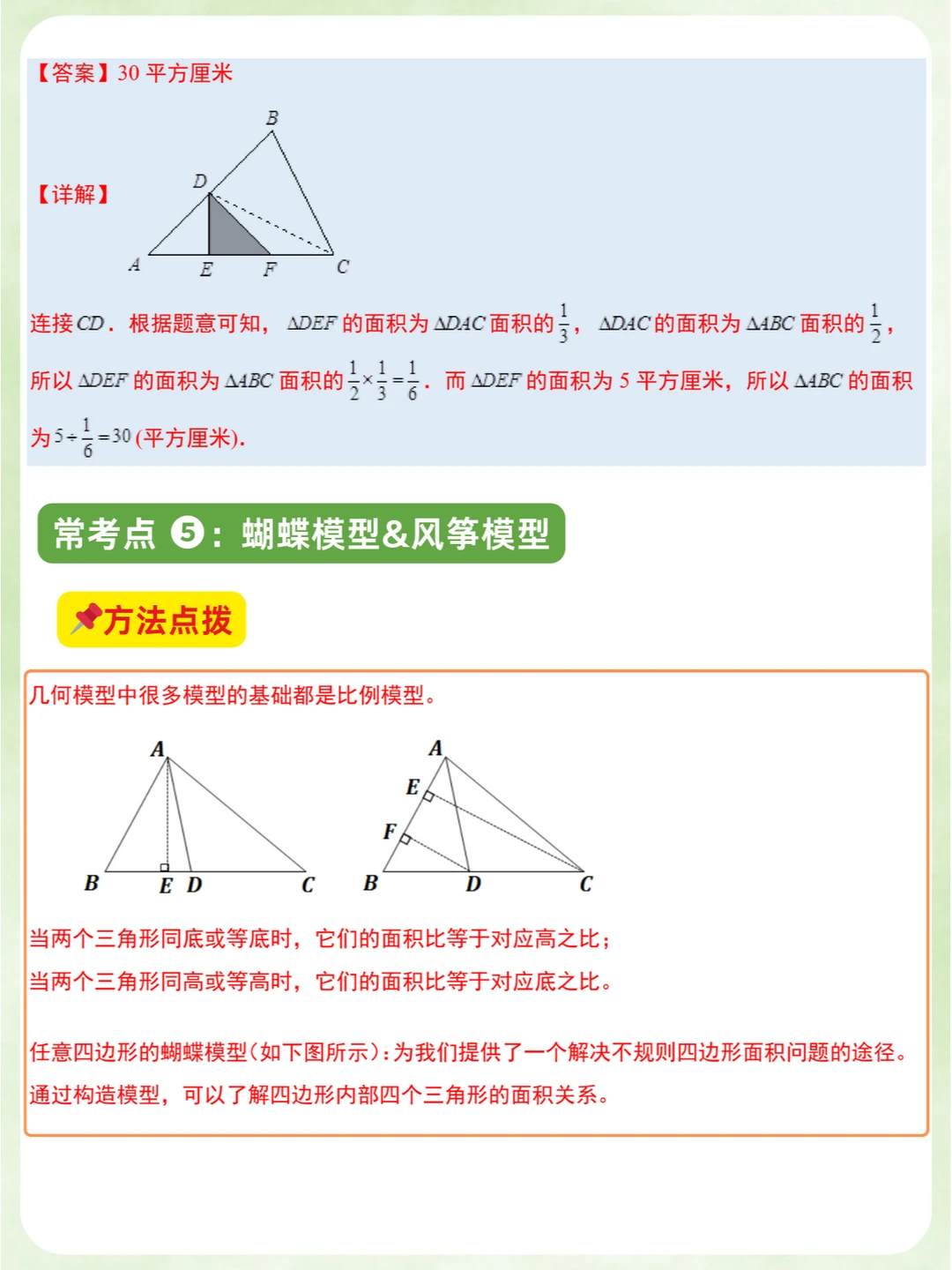
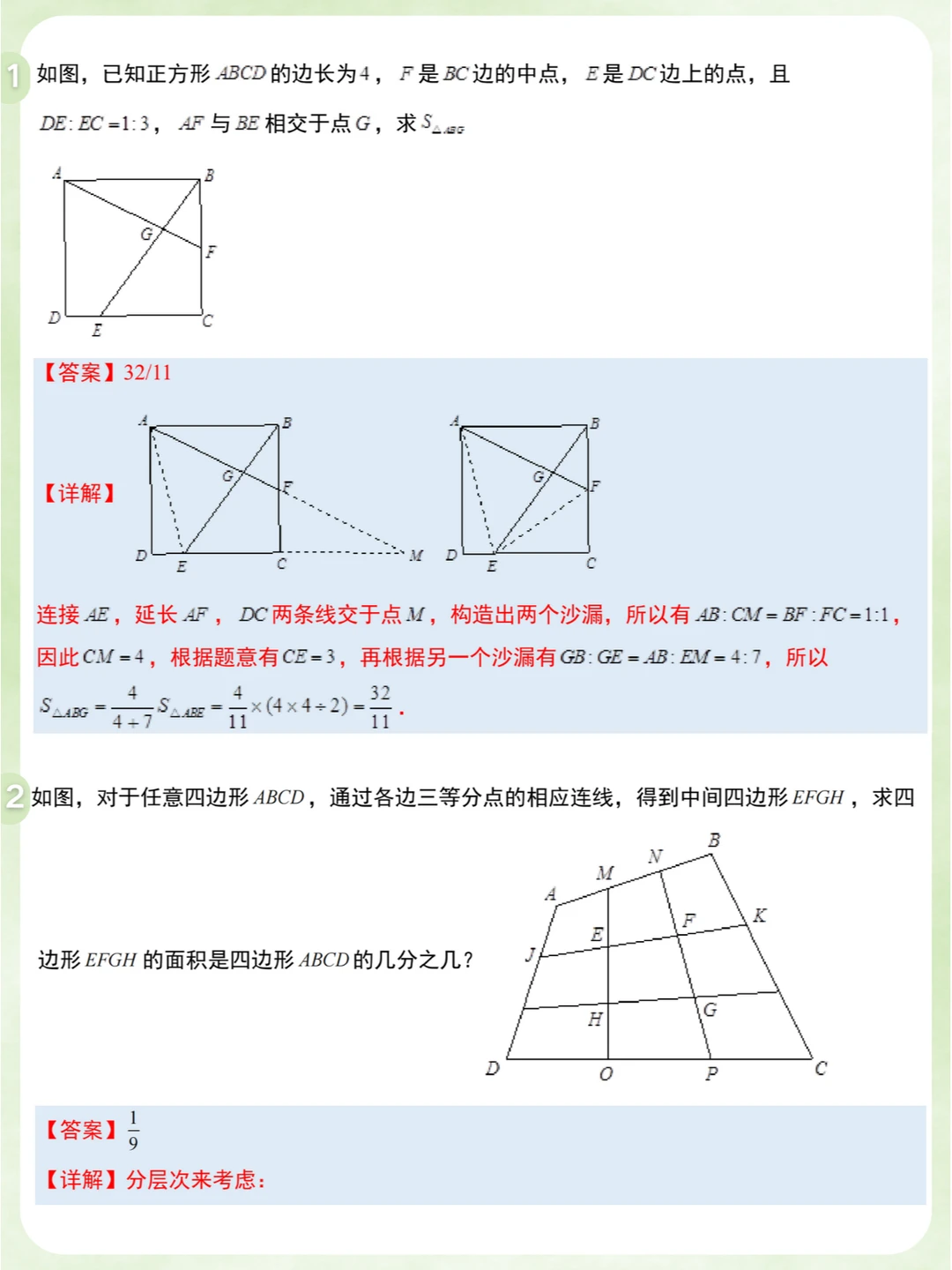
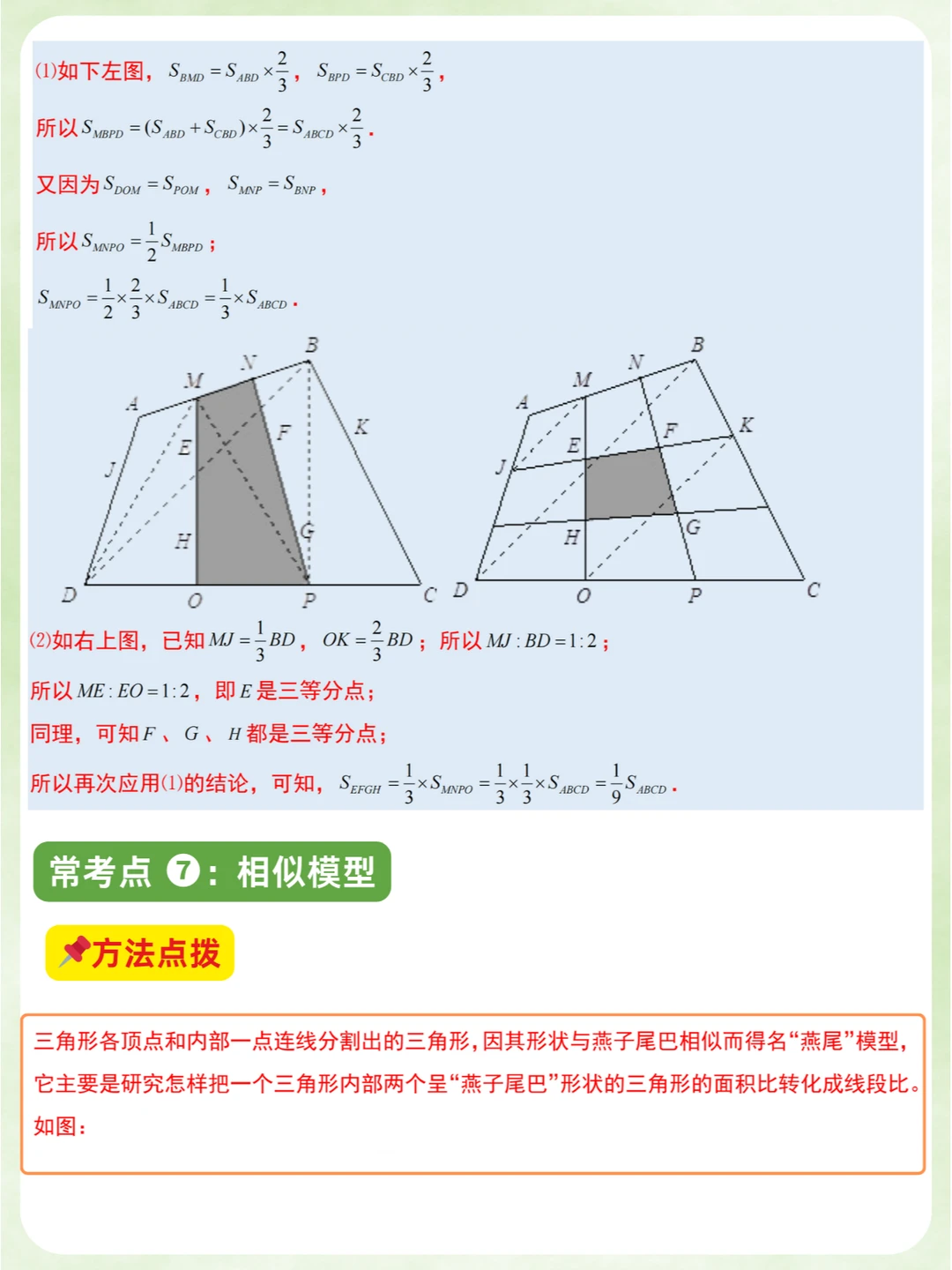
✅小学奥数：小升初名校常考7种典型几何模型✅知识点汇总梳理➕题型讲解🎉 📌这次给大家梳理汇总的是小学升学阶段常考的七种典型几何模型： 1️⃣一半模型 2️⃣等高模型 3️⃣等积变形 4️⃣鸟头模型、 5️⃣蝴蝶模型（风筝模型） 6️⃣相似模型 7️⃣燕尾模型 📌【小学几何模型学习过程中的难点】 1️⃣复杂图形的分解与组合 一些综合的几何问题可能涉及多个图形的拼接或分割，需要具备敏锐的观察力和分析能力。 比如，求不规则多边形的面积，可能需要将其分解为多个常见图形。 2️⃣公式的灵活运用 不仅要记住各种图形的面积、周长公式，还要知道在不同情境下如何选择和变形使用。 例如，已知圆的周长求面积，就需要先通过周长求出半径。 3️⃣等量代换的思想 在几何证明和计算中，常常需要通过等量关系进行代换求解。 📌【如何解决这些重难点学习过程中的问题呢？】 👉对于解决复杂图形的分解与组合问题： 1️⃣学会分类：将复杂图形按照其基本构成元素进行分类，比如是由三角形、四边形还是圆形组合而成。 2️⃣逐步拆解：从图形的一个明显特征或容易入手的部分开始，逐步将其分解为简单的图形。 3️⃣多做图形变换练习：通过对基本图形进行平移、旋转、对称等操作，培养对图形变化的敏感度。 👉对于公式的灵活运用问题： 1️⃣推导公式：不仅要记住公式，还要自己动手推导一遍，理解公式的来源和原理。 比如圆的面积公式 S = πr²，通过将圆分割成无数个小扇形再拼接成近似长方形来推导。 2️⃣一题多解：针对一个问题，尝试用不同的公式和方法求解，加深对公式的理解和运用能力。 3️⃣定期复习和总结：整理不同图形的公式以及适用条件，对比相似公式的差异。 👉对于等量代换思想的运用问题： 1️⃣寻找中间量：仔细分析题目，找出能够连接不同量的中间桥梁。 比如在两个等式中，如果都包含同一个量，那么这个量就可以作为中间量进行代换。 2️⃣绘制等量关系图 用图形的方式将题目中的等量关系表示出来，直观清晰。 例如，A = B，B = C，可以用箭头将它们的关系表示出来，便于发现代换的路径。 3️⃣多做专项练习 集中练习等量代换的题目，熟悉常见的题型和解题思路。 可以从简单的等量关系开始，逐渐增加难度。