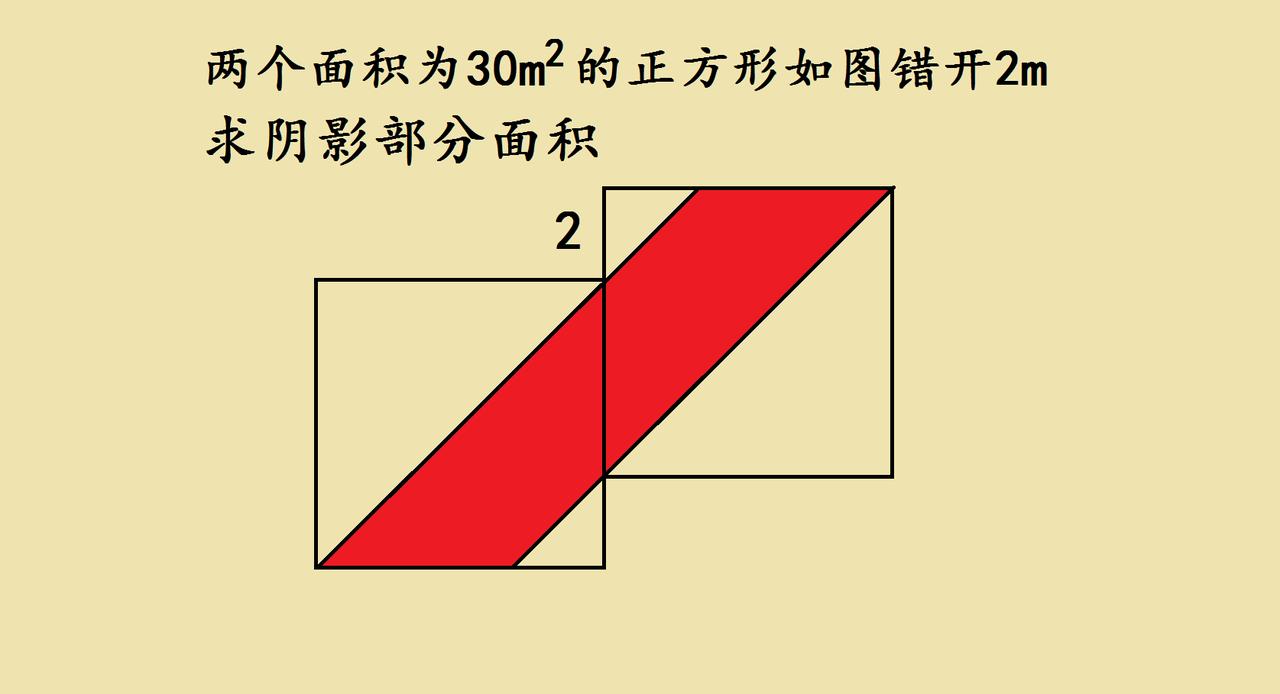
【正方形错位的几何之谜】 最近在研究一道小升初培优题，两个相同的正方形交错摆

【正方形错位的几何之谜】 最近在研究一道小升初培优题，两个相同的正方形交错摆放，中间形成了红色的阴影区域。题目给出了错位的距离，要求求出阴影部分的面积。 这道题看似简单，却蕴含着巧妙的解题思路。我首先观察图形的结构，发现阴影部分的形状并不规则，直接计算似乎行不通。 突然，我想到可以利用图形的对称性来解决。两个正方形的面积相同，错位的距离也已知，或许可以通过平移或旋转来找到隐藏的关系。 经过一番思考，我意识到这道题的关键在于发现阴影部分与正方形面积之间的联系。通过观察图形的重叠部分，我开始寻找可以相互抵消的区域。 就在我快要放弃的时候，一个念头闪过：这道题可能需要用到"等量代换"的思想。把复杂的图形分解成简单的部分，再重新组合起来。 最终，我找到了一种巧妙的方法，将阴影部分的面积与已知条件联系起来。这道题的解题思路其实很简单，只是需要换个角度看问题。 这道题让我明白，有时候看似复杂的几何问题，只要找到正确的解题思路，就能迎刃而解。学习数学就像探索迷宫，需要耐心和智慧。